Experiment 1: To determine resistivity of two / three wires by plotting a graph for potential difference

Experiment 1: To determine resistivity of two / three wires by plotting a graph for potential difference versus current.

Objective:

To determine the resistivity of two wires by plotting a graph for potential difference versus current.

Required Apparatus : 

Two resistance wires, a voltmeter (0-3)V and an ammeter (0-3 se) A of appropriate range, a battery/battery eliminator, a rheostat, a meter scale, a one-way key, connecting wires, and a screw gauge.

Theory / Formulae

According to Ohm’s Law:

$V \propto I \Rightarrow V = IR \Rightarrow R = \frac{V}{I}$

Resistivity \rho is given by:

$\rho = \frac{R \cdot A}{L}$

where:

• R: resistance from V-I graph
• $A = \pi r^2 = \frac{\pi d^2}{4}$ : cross-sectional area
• L : length of the wire

Circuit Diagram : 

Observations:

• Range of ammeter = (0 – 3) A
• The least count of ammeter = 0.05 A
• Range of voltmeter = (0 -3) V
• The least count of voltmeter = 0.05 V
• The least count of metre-scale (L.C.) =0.1 cm

L.C. of the given screw gauge:-

Pitch of screw gauge = 1 mm

Total number of divisions on the circular scale = 100

L.C. of the given screw gauge = Pitch / No. of divisions on the circular scale

= 0.01 mm = 0.001 cm

For 1st wire:

Length of the given wire, L= 15 cm = 0.15 m

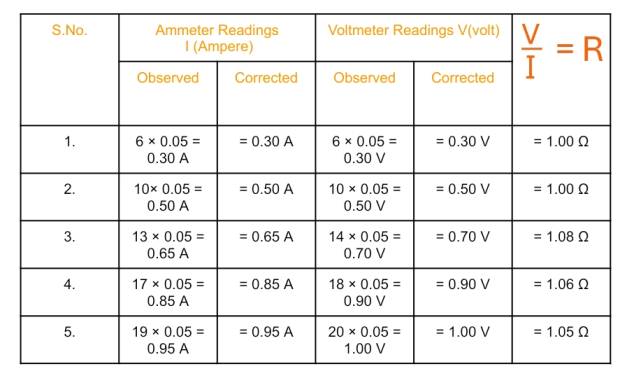
Observation Table for Resistance : 

Mean value of resistance, R= 1+1+1.08+1.06+1.05/5 = 1.04 ohm

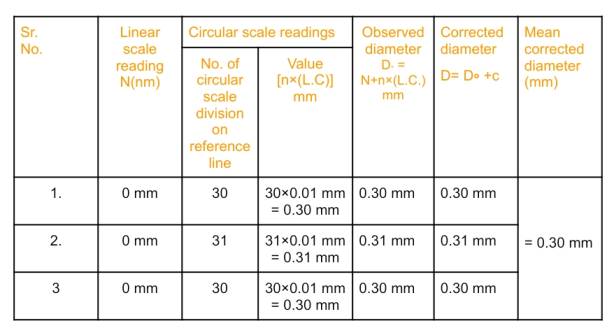
Table for Diameter of wire:

Calculation for Specific Resistance:

$\rho = \frac{R\pi D^2}{4L} = \frac{1.04 \times 3.14 \times (3 \times 10^{-4})^2}{4 \times 0.15} \text{ } \Omega\text{-m}$

$\rho= 48.98 \times 10^{-8} \text{ } \Omega\text{-m}$

Standard value of the specific resistance of the material (Constantan) of the given wire

$\rho_0 = 49 \times 10^{-8} \text{ } \Omega\text{-m}$

Percentage error =$ \frac{\rho_0 - \rho}{\rho_0} \times 100 \% = \frac{(49 - 48.98) \times 10^{-8}}{49 \times 10^{-8}} \%$

Percentage error= 0.04 %

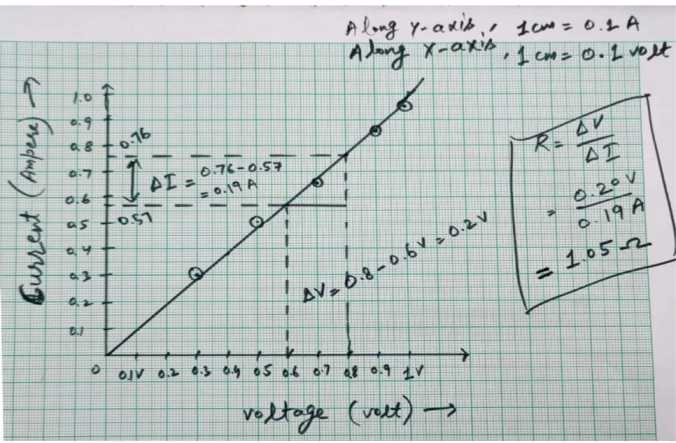
Graph – Potential difference versus Current

For 2nd wire:

Length of the given wire, L= 29cm = 0.29cm

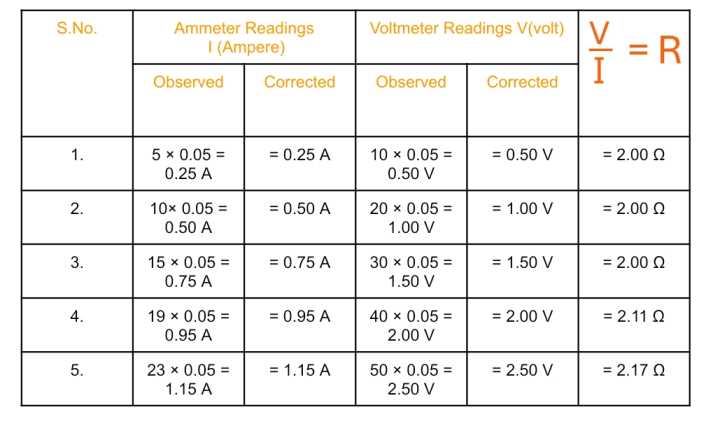
Observation table for Resistance:

Table for Diameter of wire:

Calculation for Specific Resistance: 

$\rho = \frac{R\pi D^2}{4L} = \frac{2.06 \times 3.14 \times (3 \times 10^{-4})^2}{4 \times 0.29} \text{ ohm-m}$

$\rho= 50.19 \times 10^{-8} \text{ } \Omega\text{-m}$

Standard value of the specific resistance of the material (Constantan) of the given wire

$\rho_0 = 49 \times 10^{-8} \text{ } \Omega\text{-m}$

Percentage error =$ \frac{\rho - \rho_0}{\rho_0} \times 100 \% = \frac{(50.19 - 49) \times 10^{-8}}{49 \times 10^{-8}} \%$

Percentage error = 2.43 %

Graph – Potential difference versus Current:

Result : 

• Resistance of first wire from table = $1.04 \Omega$ and from graph $1.05\ \Omega$
• Resistivity of 1st wire = $48.98 \times 10^{-8}\ \Omega\text{-m}$
• Percentage error = 0.04%
• Resistance of 2nd wire from table = $2.06 \Omega$ and from graph = $2.00\ \Omega$
• Resistivity of 2nd wire = $50.19 \times 10^{-8}\ \Omega\text{-m}$
• Percentage error = 2.43%

Precautions:

• The connection should be neat, clean, and tight.
• Thick connection wires should be used for the connections.
• The voltmeter and ammeter should be of proper range.
• A low-resistance rheostat should be used.
• The key should be inserted only while taking observation to avoid heating of resistance.
• At one place, the diameter of the wire should be measured in two mutually perpendicular directions.
• The wire should not make a loop.

Source of Error:

• The instrument connections may be loose.
• Thick connection wires may not be available.
• Rheostat may have high resistance.
• The wire may not have uniform thickness.
• The screw gauge may have faults like a 'backlash' error and a wrong pitch.